A general recurrent state space framework for modeling neural dynamics during decision-making

タスク

既存手法

Diffusion drift model (DDM)
- 感覚情報が時間とともに蓄積され, 情報量が閾値を越えたときに行動を選択すると仮定
  - 閾値には上限と下限があり, それぞれが二肢に対応
- DDMの発展として出力を高次元に拡張したもの, 敷値が時間とともに変化するもの, 単一試行だけでなくこれまでの試行を全て考慮するもの等が提案されている

提案手法

Recurrent switching linear dynamical systems (rSLDS)モデルにDDMの仮定を導入して (パラメータに縛りを設けて)拡張し本タスクに適用
- rSLDSは状態空間モデルの一種で連続の潜在状態 \(x_t\)が前の時刻の状態 \(x_{t-1}\)と離散の潜在状態 \(z_t\)ごとの変数 \(b_{z_t}\), その時刻の入力 \(u_t\)によって決まると仮定
- 図1Cにグラフィカルモデルを示す
- 現在時刻の\(z_t\)は前の時刻の \(x_t\)と \(z_t\)で決まり, 遷移確率として複数クラスのロジスティック回帰等が用いられる
- 出力 \(y_t\)が潜在状態 \(x_t\)に依存して決まる (ポアソン分布を仮定)
提案手法では3つの潜在状態 \(z_t\)を導入
- 1つ目は蓄積している状態, 2つ目は上限に達した状態, 3つ目は下限に達した状態
\(u_t\)は入力の感覚情報
DDMの仮定に合わせて遷移パラメータを固定
- 連続潜在状態 \(x_t\)が一度閾値を超えた場合に離散潜在状態が蓄積から上限あるいは下限に遷移する
図1Bは本モデルからシミュレーションで生成したポアソンスパイク系列

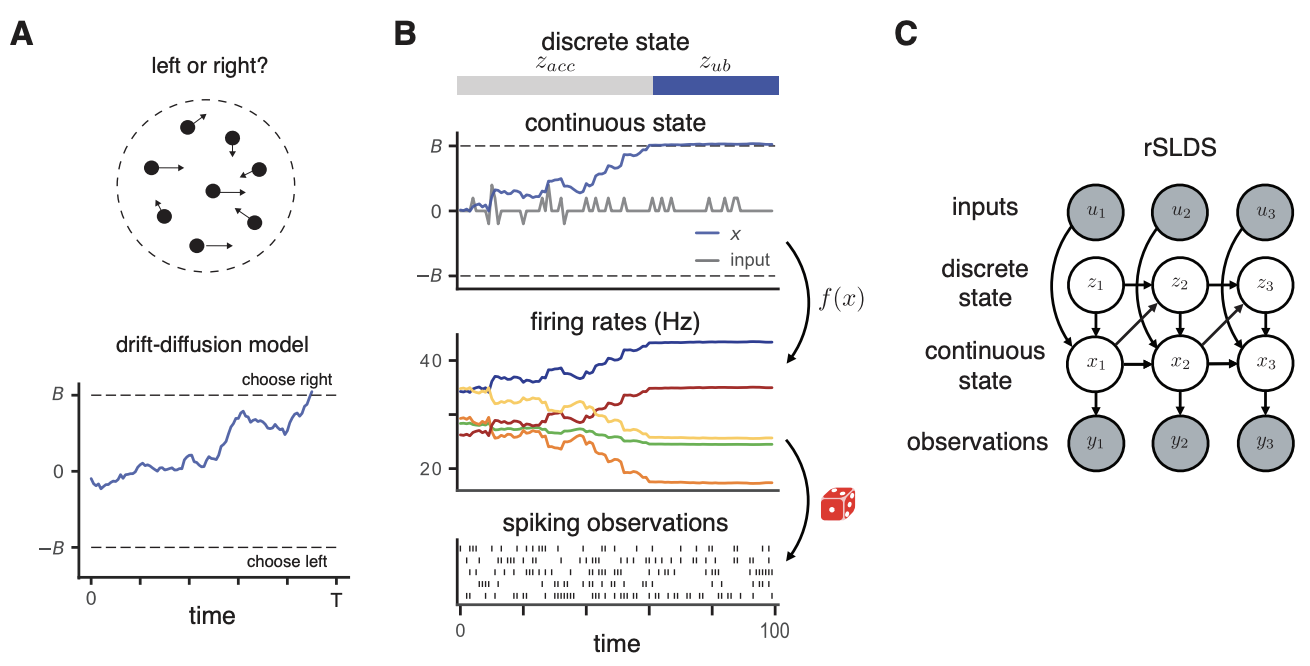
提案手法は高次元の出力, 敷値を時間変化させる, 過去の試行を考慮する等様々なDDMの仮定に合うよう拡張できる
提案手法の学習のためラプラス近似を用いた変分EMアルゴリズム vLEMを提案
- rSLDSの推論には最尤推定が用いられる\(\rightarrow\)時系列の長さに対して指数的に計算量が増加
- これに対処するため, Expectation propagation (EP)法やギブスサンプリングを用いた手法が提案されている
- しかし提案手法には直接適用できない
  - 遷移方程式にロジスティック回帰, 出力にポアソン回帰を用いているため, パラメータが共役でなくなる
- ブラックボックス変分推論 (BBVI)を用いる方法でもパラメータへの強い制約を課しているせいで性能が出ない
潜在変数に関する事後分布 \(p(x,z\vert \theta,y)\)を \(q(z)\)と \(p(x)\)に分解し \(q(z)\)を変分近似, \(q(x)\)をラプラス近似する

実験

シミュレーションデータに対する提案手法の推定結果を図3Aに示す
- 図3A上部に離散潜在状態のGround Truth \(z\)と推定結果 \(\hat{z}\)を比較
- 図3A下部に2つ (赤・青)の連続的な潜在状態についてGround Truth \(x\) (実線)と推定結果 \(\hat{x}\) (点線)を比較
- 網掛け部分は事後分布 \(q(x)\)の標準偏差の2倍を表す
- 提案手法は真の潜在状態を正確に再現できている
ランダムドットモーション実験で取得したデータを用いた結果を図6に示す
- コンピュータ画面上の多数の白い点がランダムに動く刺激 (ランダムドットモーション)を見せ, その刺激の全体としての動きの方向 (あるいは右)を被験者に判断させる
- 状態遷移の閾値が試行によって変わるケースを考える
- 図6Cの黒線を見ると連続潜在状態 \(x\)が収束するタイミングが試行によって変化しているのがわかる