Temporal Logic Point Processes
タスク
- 過去のイベント系列と事前知識に用いて将来イベントがいつ, なぜ起こるのか予測する
- 医療分野において治療の効果を予測
- 例えば敗血症については”敗血症性ショックが起こる”と”血圧が下がる”, “血圧をコントロールする”と”敗血症性ショックによる生存確率が上がる”等の事前知識がある
- このような事前知識は論理式で記述できる
- クレジットカードの不正利用の検出
- 不正利用は少数なためラベルが少ない&完全でない
- そこで不正利用の場合”大きな買い物”もしくは”同じ商品の大量購入”しがちといったドメイン知識を利用
- 医療分野において治療の効果を予測
予備知識: 時相論理
- 一階述語論理
- とある群 \(C=\{c_1,c_2,...\}\)に対して定義される論理関数 \(x(\cdot)\in\{0,1\}\)を考える
- 例えば \(\texttt{smoke}(c)\), \(\texttt{Friend}(c,c')\)など
- 論理関数はあるものの性質や関係を表す
- 時間述語は群 \(C=\{c_1,c_2,...\}\)と時刻 \(t\)に対して定義される論理関数 \(x(\cdot,\cdot)\in\{0,1\}\)
- 時間述語の軌跡は二つの状態からなる連続確率過程と見做せる
- 例えば時間述語 \({\text{NormalBloodPressure}(c,t)}\)は時刻 \(t\)における患者 \(c\)の血圧が正常か否かを表す
- 状態遷移の時刻は確率的
- 論理関数 \(x(t)\)は下図の通り連続的なものと瞬間的なもの両方ある
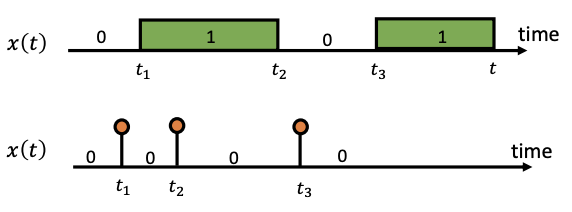
- 時間相関
- 先行研究ではタイムインターバルのペアについて13種類の関係 \(\{r_1,...,r_{13}\}\)を定義している
- 各々の関係についてステップ関数とデルタ関数の複合関数が論理関数として定義されている (表1)
- この定義を用いて述語 \(x_A\)と \(x_B\)のタイムインターバルを考慮した論理関数を導出する
提案手法
- \(d\)つの時間述語 \({\bf X}(t)=\{x_1(t),...,x_d(t)\}\)が与えられているとする
- 例えば医療分野では下図のような例が考えられる
- 時間述語 \(x_u(t)\)は例えばある薬を投薬したかどうか \(\text{UseDrug1}(t)\)や血圧などある時刻 \(t\)の患者の状態 \(\text{NormalBloodPressure}(t)\)を表す
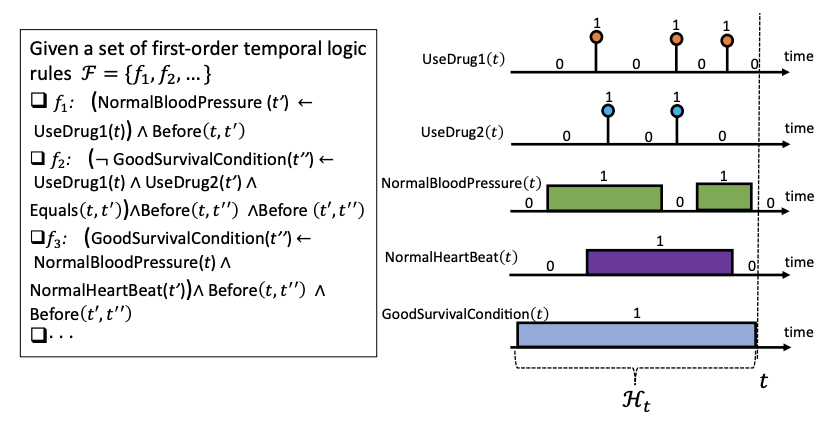
- さらに事前知識を表す論理命題の組 \(\mathcal{F}=\{f_1,f_2,...\}\)が合わせて与えられている
- 例えば医療分野の例の一階論理式は \((\text{GoodSurvivalCondition}(t)\leftarrow\text{NormalBloodPressure}(t)\land\text{NormalHeartBeat}(t))\land\texttt{Before}(t,t'')\land\texttt{Before}(t',t'')\)
- 本稿ではこれらの論理式を点過程に導入する手法を提案する
- 各々の時間述語 \(x_u(t)\)に対して2つのインテンシティ \(\lambda_u(t)\), \(\mu_u(t)\)を導入
- これらのインテンシティは状態遷移時刻における時間述語の系列 \(\mathcal{H}(t)=\{x_u(0), x_u(t_1),...,x_u(t_n), x_u(t)\}\)に依存
- 時間述語は \([0,t_1)\), \([t_1,t_2)\), … のタイムインターバル内で一定
- 時間述語が0の場合は\(\lambda_u(t)\), 1の場合は\(\mu_u(t)\)を使用
- これらのインテンシティは状態遷移時刻における時間述語の系列 \(\mathcal{H}(t)=\{x_u(0), x_u(t_1),...,x_u(t_n), x_u(t)\}\)に依存
- 論理命題 \(\mathcal{F}\)を用いて時間述語のインテンシティを記述
- 述語 \(x_A\), \(x_B\)が真なら \(x_C\)も真であり従って \(x_A\)は \(x_B\)より前に起こり \(x_A\), \(x_B\)は \(x_C\)より前起こるという命題 \(f_1\)が与えられたとする
\(f_1 : (C\leftarrow A \land B) \land (A \text{ before } B) \land (A\text{ and }B\text{ before }\text{C})\) - 例として時間述語 \(x_A\)と \(x_B\)に基づいて \(x_C\)のインテンシティを推定するケースを考える
- \(f_1\)で定義されている \(x_A\), \(x_B\)の複合的な影響をタイムインターバル同士の時間相関の定義を用いて \(\delta_{f_1}\)でモデル化する
- \(\lambda_C(t)\)を全てのタイムインターバルの組み合わせについて \(\delta_{f_1}\)の和を取りこれを用いてインテンシティを記述
- 各々の倫理式の確からしさを表すパラメータ \(w_{f_1}\)を導入し上述の和と掛け合わせる
- もう一つのインテンシティ \(\mu_C(t)\)についても同様の定式化
- 述語 \(x_A\), \(x_B\)が真なら \(x_C\)も真であり従って \(x_A\)は \(x_B\)より前に起こり \(x_A\), \(x_B\)は \(x_C\)より前起こるという命題 \(f_1\)が与えられたとする
- 倫理式 \(f_1\)が複数ある場合, 全ての倫理式 \(\{f_1,f_2,...\}\)について(9)式を足し上げたものをインテンシティ \(\lambda_C(t)\)とする (\(\mu_C(t)\)も同様)
- \(x_C(t)\)が0の場合と1の場合に分けて尤度を書き下し, 対数尤度を最大化するようなインテンシティのパラメータを学習
- 尤度関数に含まれる積分は数値近似
実験
- MIMIC-IIIデータを使用
- 少数のイベント履歴を用いて生存率を予測
- 医師の知識を元に敗血症の病原についての倫理式を定義 (表3)
- 表4では生存率, 表5では生存時間の予測精度をMAEで比較
- 図6では倫理式の確からしさを表すパラメータ \(w_{f_1}\)を可視化