Getting a CLUE: A Method for Explaining Uncertainty Estimates

タスク

予測の不確実性を説明する
不確実性が小さくなるよう, 入力を修正する
- 元の入力と修正された入力を比較することで, 入力のうちどの特徴量が予測の不確実性に寄与しているか, 特定する
  - ローンの債務不履行リスクの予測において, 不確実性に寄与する属性 (過小評価グループ)を特定する
  - 患者が治療を受けるべきかどうか予測するシステムにおいて, 不確実性に寄与する特徴量を特定する

既存手法

説明性を考慮するための2つのアプローチ
1. LIMEなどモデルそのもの (の一部)を決定木, 線形回帰などの説明可能なモデルで置き換える手法
  - 近似の正しさが問題になる
2. 反事実 (counterfactual)を用いた説明
  - 反事実は因果推論の文脈でよく使われるが, 説明性の領域ではもう少し緩い定義で使われる
  - “どの特徴量を除いたら説明性が上がるか”“どの特徴量を変化させたらモデルの出力が変わるか”というほどの意味
  - 反事実を使ったアプローチは近似が要らないのが利点
しかし, 予測の不確実性を説明する手法は少数
不確実性の起源は(i) データに含まれるノイズと(ii) 未知のデータの2つある
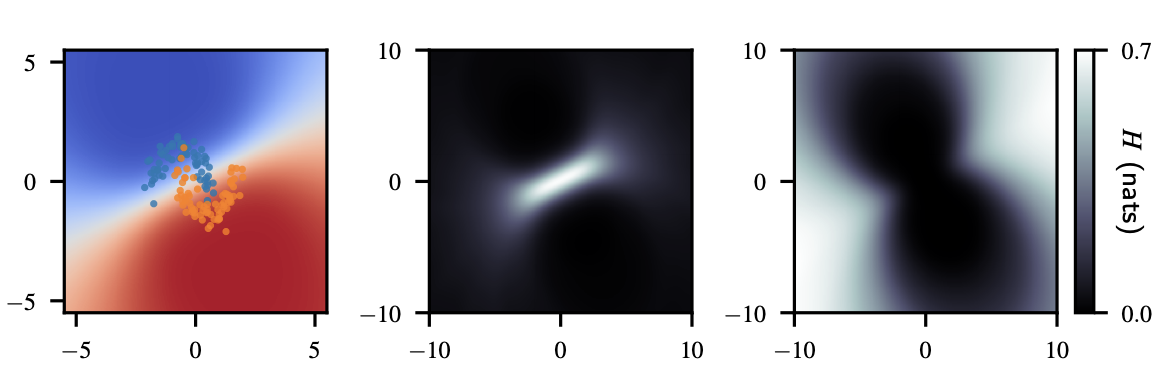
図はMoonsデータセットに対してベイジアンロジスティック回帰をかけた結果
- 左が入力のデータ, 真ん中が回帰曲線, 右が不確実性
- 真ん中の回帰曲線からわかるように, 2つのクラスに重なりがあるため, このようなデータは分類が難しい
- また, 右の図を見ると, 学習データに含まれない部分 (白の部分)は予測の不確実性が高くなっている

元論文図2より引用

不確実性を考慮したニューラルネットワークとして, 重みを確率分布でモデル化するベイジアンニューラルネットワーク (BNN)が提案されている
不確実性の説明性を考慮した手法として, Uncertainty Sensitivity Analysis [Depeweg et al., 2017]が唯一提案されている
- 不確実性の測度 \(\mathcal{H}\)に対する入力の寄与を表す関数を線形回帰の混合モデルで近似
- しかし, BNNのような非線形関数を線形関数で近似するのは無理がある
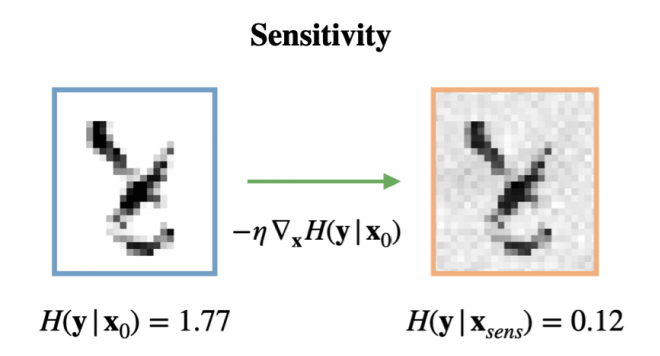
- この手法をMNISTへの適用した結果を下図に示す
- 特に高次元が高次元な場合, 意味のある学習ができなくなってしまう

元論文図3より引用

提案手法

予測の不確実性に寄与する入力を推定する手法を提案
- 予測の不確実性を下げるためにどのように入力を修正すればいいか?という問いに答える
近似を使ったアプローチ, 反事実を使ったアプローチのうち, 今回は後者を選択
- 上図のMoonsデータの結果からもわかるように, 出力が線形でも出力の不確実性が線形とは限らない
- 従って, モデル自体をシンプルなモデルで近似する手法をそのまま適用することができない
提案手法は創薬分野における論文 [Rafael et al., 2018]を参考にしたもの
- 分子のSMILES (化学構造の文字列表現)をエンコードし, 潜在空間に埋め込む
- SMILESを復元するデコーダと物性値を予測するMLPと結合
- とある物性値を最適化する薬の探索をする場合, 愚直にやろうとすると, 巨大かつ離散の探索空間における最適化が必要になる
- この問題を連続的な潜在空間における探索に帰着させた点がポイント
BNNの入力 \({\bf x}_0\)を確実性を最小化するような新たな入力 \({\bf x}_{\text{CLUE}}\)に変換するVAEを学習
この新たな入力を論文中では”反事実”と呼んでいる

元論文図3より引用

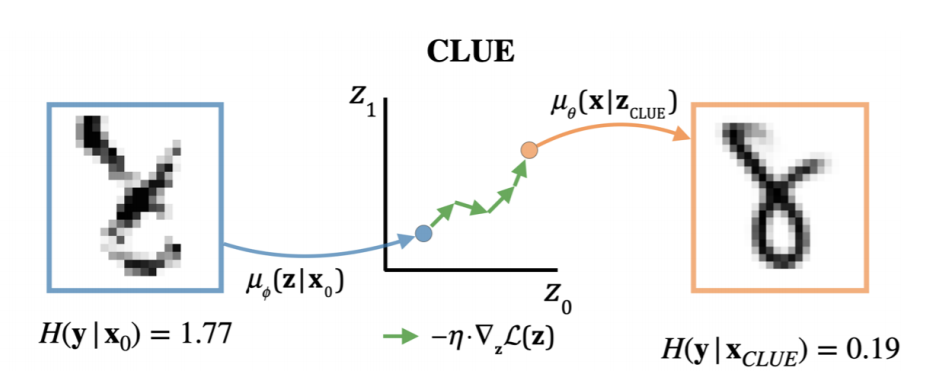
入力 \({\bf x}_0\)と似ていて, かつ, 不確実性 \(\mathcal{H}\)を最小化するような反事実 \({\bf x}_{\text{CLUE}}\)を出力する
元の入力 \({\bf x}_0\)と \({\bf x}_{\text{CLUE}}\)の差 \(\Delta{\bf x}\)を取ることで, 入力のうちどの箇所が不確実性に寄与しているか (悪さをしているか)判断できる

実験

LSATの累犯データ, COMPASの成績データを使ってユーザ実験を行う
メインの調査の前にパイロット・テストを行う
- データセットにベイジアンニューラルネットワーク (BNN)を適用して各データ点の不確実性を推定し, それに応じてデータ点を不確実/確実に分類しておく
- データセットからデータ点をランダムにサンプルしtest pointとする
- 不確実と判断されたデータセットの中から, test pointと関連するデータ点を抽出し, context pointとする
メインの調査では, 新しいデータ点に対してユーザに不確実 or 確実を判断させる
- 各々のcontext pointについて, 各手法を用いて入力 \({\bf x}\)を修正
- ユーザにtest point, 修正されたcontext pointを見せる
- その後, 新しいデータについて確実 or 不確実の判断をしてもらう
提案手法のCLUEを含む4つの手法を考え, 各々に10人のユーザをアサイン
Context pointの修正を行う際, ベースラインとして以下の3つの手法を考慮
1. Uncertainty Sensitivity Analysis [Depeweg et al., 2017]
2. 人手
3. ランダム
人手がランダムと同程度の精度
- このタスクにおいては人の直感が当てにならない
Uncertainty Sensitivity Analysisが最も悪い結果
- Sensitivity Analysisによる入力の修正はかえって判断を狂わす
提案手法のCLUEが最も良い精度

査読