Multi-relational Poincaré Graph Embeddings
タスク
- 階層データのモデル化
- ナレッジグラフ等のグラフデータは複数種類の階層を含む
例: ライオンは動物の食物連鎖の最上位に位置するが, 哺乳類の分類を表すツリーでは最下位に位置する
- ナレッジグラフ等のグラフデータは複数種類の階層を含む
既存手法
- 階層データを双曲空間に埋め込む手法が提案されている
- 双曲線空間は離散木の連続的なアナロジーとして捉えることができ, 階層データのモデル化に適している
- ゼロ曲率の空間 (ユークリッド)の代わりに一定の負の曲率を持つ空間 (ハイパーボリック)でツリー状の構造をモデル化
- ニューラルネットを用いた埋め込みタスクにおいて有効性が確かめられている
- 双曲幾何学は表現学習において広く用いられている
- 階層的な多関係グラフデータを双曲空間に埋め込むアプローチが提案されている
- しかし, ユークリッド距離を使う手法を精度で下回っている
- 多関係グラフデータを双曲空間で表現する場合, 異なる関係における異なる階層を表現できるように各ノードの埋め込み表現を学習する必要がある
- 例: ある関係の下ではツリーの根に近いノードが, 別の関係の下ではリーフノードになる等
- 多関係データをモデル化するための手法として, DistMult, ComplEx, TuckER等のバイリニアモデルが提案されている
- これらの手法は類似性指標としてユークリッド内積を用いている
- ユークリッド内積と対応関係にある距離の指標は双曲線領域においては存在しない
- TransEやSTransEなど, ユークリッド距離を使用して類似性を測定するアプローチもある
- ユークリッド距離を双曲線領域における距離に変換することもできるが, 今のところ予測精度が低い
提案手法
- ポアンカレ球に階層的な多関係データを埋め込むための手法 MuRPを提案
- 特定の点を中心に半径が大きくなる超球を考える
- ノードの埋め込みを決める関係ごとのパラメータをメビウス積・メビウス加算で学習
- 以下の2つのアイデアにヒントを得て, 多関係グラフ埋め込みのための新しい基礎スコア関数を提案
- GloVeの双曲バージョンであるポアンカレGloVeではユークリッド距離をポアンカレ距離に置き換えて双曲空間における距離として使っている
- 単語埋め込みの手法 Word2Vec の良く知られた性質として加法構成性がある
- 例: 王の埋め込みベクトルから男のベクトルを引き, 女のベクトルを足すと女王のベクトルに近づく
- Word2vecではある特定の関係を共有するすべての単語対 (王と男, 女王と女)は, ベクトル空間内で同じオフセットベクトルで関連付けられるように埋め込まれる
- オフセットベクトルは埋め込み空間において「王」-「男」, 「女王」-「女」の引き算をした残差のベクトル
- このアイデアは本研究のタスク (多関係グラフのノード埋め込み)にも適用することができる
- 基礎スコア関数は次式で定義される
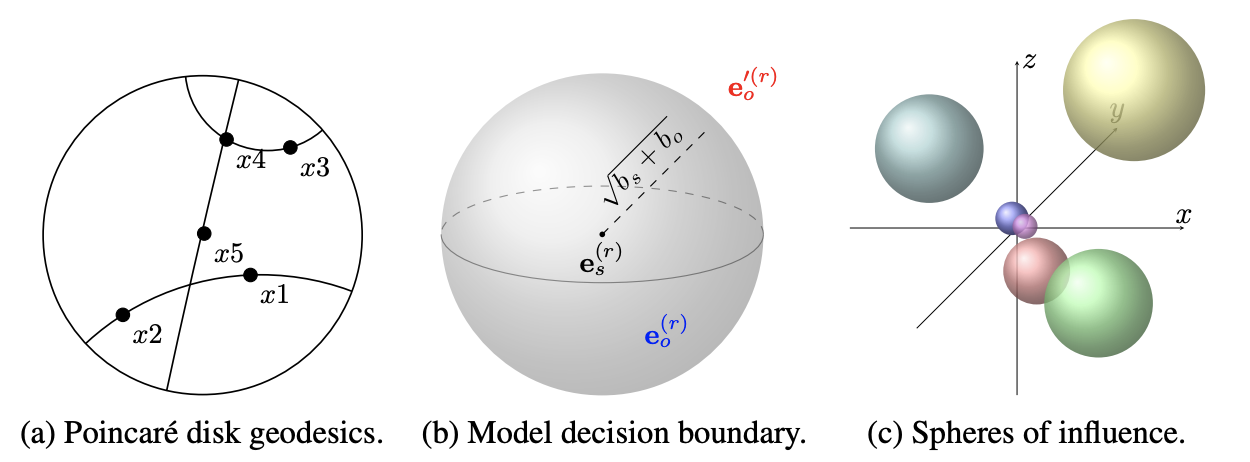
\(\phi(e_s,e_o)=-d({\bf e}_s^{(r)},{\bf e}_o^{(r)})^2+b_s+b_o=-d({\bf R}{\bf e}_s,{\bf e}_o+{\bf r})^2+b_s+b_o\)- バイアス \(b_s\), \(b_o\)は \({\bf e}_s^{(r)}\)を中心とした超球面の決定境界の半径を決める
- 関係性に応じて調整をかけた距離 \({\bf e}_s^{(r)}\)が半径 \(\sqrt{b_s+b_o}\)の超楕円に収まる場合, ノード \(e_s\)と \(e_o\)は関係 \(r\)によって関連づけられていると予測される
- この距離関数はTransE, STransE等で使われているものと似ているが, エンティティ固有のバイアスを導入した点が新しい
- エンティティを空間上の点とみなすのではなく, 埋め込みベクトルで与えられた中心を囲むエンティティ固有の影響範囲を定義するバイアスを用いる
- 球体間の重なりがエンティティ間の関連性を表す
- すなわちそれぞれの関係は, 影響力のある球体を空間的に動かしていると考えることができる
- 各関係の下でつながっている主語と目的語のエンティティの球のみが重なるように影響力の球を移動させる
- 双曲空間への埋め込みの効果を評価するため, 実験では \(d({\bf e}_s^{(r)},{\bf e}_o^{(r)})\)をユークリッド距離に置き換えた手法 MuREとの比較を行なった
- 学習の際はまずデータ蒸留のための手法を使って全ての三つ組 \((e_s,r,e_o)\)について逆の関係 \((e_o,r^{-1},e_s)\)を生成
- 各々の三つ組について \(k\)つのネガティブサンプルを生成
- これらのサンプルを使ってベルヌーイ対数尤度を最大化するモデルのパラメータを見つける
- 関係を満たすエンティティと満たさないエンティティを分類するタスクとみなす
実験
- 標準的なWN18RRおよびFB15k-237データセットを用いて知識グラフのリンク予測タスクにおける性能を比較
- FB15k-237データセットは実世界の事実を集めた Freebaseのサブセット
- WN18RRは WordNetのサブセットで, 単語間の関係の階層的な集合
- モデルの評価には, リンク予測の分野で標準的に用いられている評価指標 Mean reciprocal rank (MRR), hits@k, \(k\in\{1, 3, 10\}\)を用いる
- 表1は両データセットで得られた結果
- MuREは非階層型のFB15k-237データセットでわずかに良い結果
- MuRPは階層的な関係を含むWN18RRで優れた性能を発揮
- 比較的低い埋め込み次元 (\(d=40\))でもこの結果は変わらず
- 双曲線モデルが複数の階層を簡潔に表現できるため
- 図4は「asia」という単語に対する40次元の主語埋め込みと, 階層的なWN18RR関係has_partの1500個のオブジェクト埋め込みのランダムなサブセットを2次元に射影したもの
- ここでは主語 \(e_s\)と目的語エンティティ \(e_o\)の埋め込みを可視化
- MuREでもMuRPでも, 関係固有の変換を行うことで真の目的語と偽の目的語が分離されている
- ポアンカレ距離に基づく MuRPモデルでは, 原点からの距離が長くなると埋め込みが円の外縁に向かって移動する
- 大雑把に言うと, 外縁付近のエンティティを分離し区別するためのより大きなスペースがある