KDD 2021 Keynote Report
国際会議KDD2021の基調講演の概要メモ
Keynote: On the Nature of Data Science
Jeffrey Ullman (Stanford University) Website
- 講演の前半はUllman氏の最近の論文 The Battle for Data Scienceとかなりかぶる内容
- データサイエンスはコンピュータサイエンスの一分野であり, 特に大規模データの処理を得意としてきた
- データサイエンスの立ち位置を説明する際, このようなベン図がよく使われる
- ただしこのベン図にはいくつかミスリーディングな点がある
- “Substantive expertise”はより正確には”Domain knowledge”
- “ハッキングスキル”はより正確には”コンピュータサイエンス”
- アルゴリズムの実装を行わない理論研究は本当に”Traditional research”なのか? 少なくともデータベースコミュニティの伝統ではない
- 機械学習は「ハッキング」+「数学/統計」に位置付けられているが, 実際にはApplicationと大いに関係している
- Ullmanはより正確なデータサイエンスの立ち位置を表す新しいベン図を提案
- コンピュータサイエンスと様々な分野の科学があり, それらが交差領域にデータサイエンスが位置付けられる
- 機械学習はコンピュータサイエンスの一分野
- 数学と統計学はコンピュータサイエンスにとって非常に重要なツールであり, それらの知見に基づいて構築されるアルゴリズムによって間接的に様々な領域の科学に貢献する
- 講演の後半ではデータサイエンス分野で独自に発展した技術として局所性鋭敏型ハッシュ (LSH)とcounting distinct elementsの概要を紹介
Keynote: Data Science for Assembly Engineering
Sharon Glotzer (University of Michigan)
- Self-assembly (自己集合)とは物質が熱力学や統計力学の法則に従って自律的に組織化するプロセス
- ここで物質=原子, 分子, タンパク質等の大きな分子, DNA, ナノ粒子など
- Self-assemblyは自然界でもよく見られる普遍的なプロセス
- 一番シンプルな例は水→氷の結晶化
- もう少し複雑な例だと 脂質やタンパク質の自己組織化がある
- (a) 脂質分子がラメラ, チューブ, 小胞状構造を形成する例を模式的に表した図
- (b) タンパク質が硬く結晶性の高いラメラ, らせん状チューブ, 正20面体構造を形成する例
- (c) SDS@2β-CDがタンパク質に似た経緯で硬く面内で菱面対称性を持つラメラ, らせん状チューブ, 菱面対称12面体構造を自己組織化により形成する例
- こうした物質の自己集合を新しい素材の開発に利用する取り組みが進んでいる
- Glotzer氏のラボでは主にナノ粒子の自己集合の研究に取り組んでいる
- この分野のブレイクスルーは2015年の論文
- DNAなどの物質をボンドがわりに使うことでナノ粒子が原子と同様の構造に自己集合することがわかった
- 自己集合のプロセスは複雑でミクロレベルでは解明されていない
- 自己集合の過程で各々の分子がどう動いているのか (Assembly pathway)はわからない
- Assembly engineeringは望ましい性質を持つ物質が自己集合で自動的に作られるような設定を見つける研究
- ここで設定=ボンドとして使うDNAの長さや量, 気温や圧力などの条件
- この目的で自己集合のプロセスをシュミレーションで再現する
- Glotzer氏のラボでは粒子シミュレーションを行うオープンソースアプリケーションを複数開発している
- 粒子の形, 相互作用, 気温などの条件を色々変えて何十万回か走らせることができる
- 液体から固体になるまでの長い軌跡を追える
- 時間的粒度が高い
- Assembly pathwayの理解に教師なし機械学習モデルを利用することができる
- シュミレーションで生成したAssembly pathwayを教師なしの埋め込み手法 UMAPを使って低次元に可視化
- これにより複数のAssembly pathwayの比較が容易になる
Keynote: Safe Learning in Robotics
Claire Tomlin (University of California at Berkeley)
- クアッドローターなどの移動ロボットを規律がない環境においても安全に制御するための研究
- 講演の前半では計算論的取り組み, 後半では機械学習を用いたアプローチを紹介
- 安全性を考慮したロボットの制御においては, 後進可到達集合 (Backward reachable sets)を利用することができる
- 後進可到達集合は有限時間内に目標とする集合 (ここではシステムの危険な状態を表す集合=危険集合)に到達するような軌道を持つ状態点の集合
- 取りうる初期値のうち後進可能到達集合 \(G(0)\) (図の赤の部分)に属している状態点は有限時間内に危険集合に到達する
- 一方, 後進可能到達集合の補集合は危険状態へ到達することのない状態点の集合なので, この中から初期値を選べば安全性を確保できる
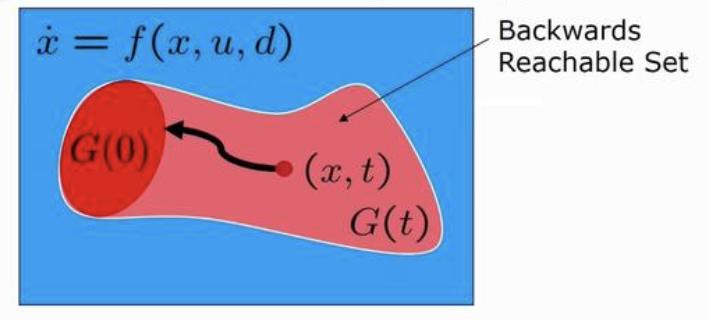
- ここでは外乱 \(d\)がある場合にシステムを安全な集合の中に入れるような制御を考える
- 外乱 \(d\)がわからない時は最も悪い (危険領域に押しこんでくる)場合を考える
- システムの状態 \({\bf x}\)は一般的に外乱 \(d\), 制御 \(u\)を用いて微分方程式 \(d{\bf x}/dt = f({\bf x},d,u)\)で表される
- Tomlin氏のチームでは時刻 \(t\)における後進可能到達集合 \(G(t)\)の計算にStanley Osherらによって提案されたレベルセット法 (Level set method)を適用
- レベルセット法は検出する境界を一次元高い補助関数のゼロ等高面とみなし, 境界の時間発展を決める偏微分方程式を数値的に解いて補助関数の形状を変更し, そのゼロ等高面を次々に検出する手法
- 時刻 \(t\)における後進可能到達集合 \(G(t)\)を補助関数 \(J({\bf x},t)\)のゼロ等高面 \(G(t) = \{ {\bf x}: J({\bf x},t)<0 \}\)で定義
- 補助関数 \(J({\bf x},t)\)はハミルトン-ヤコビ-アイザック方程式 \(-\frac{\partial J({\bf x},t)}{\partial t} = \min \{ 0,\max_u \min_d \frac{\partial J({\bf x},t)}{\partial {\bf x}} f({\bf x},u,d) \}\)の解となる
- \(J({\bf x},t)\)は符号付き距離函数
- 危険集合とそれ以外の集合の境界では \(J({\bf x},t)=0\)
- \(\vert J({\bf x},t)=0 \vert\)は時刻 \(t\)における状態 \({\bf x}\)と境界の距離
- \(J\)は危険領域の内側で負, 外側で正
- 制御の文脈においては, 符号付き距離函数を用いたモデル化によって危険の度合いがわかるという利点がある
- Tomlin氏のチームでは本手法の実装を公開 Code
- ハミルトン-ヤコビ-アイザック方程式の古典的な解法は存在しない→数値計算
- 状態 \({\bf x}\)を均一グリッド点で離散化し, あらかじめ決めた積分時間幅で繰り返し更新する
- 特に状態 \({\bf x}\)の次元が大きい場合に計算量が増大する
- このアプローチの効果を評価するため複数のクワッドローターの衝突回避実験を行った
- 4つのクワッドロータを4人の学生が操作
- クワッドロータに搭載されたオートパイロットで衝突を回避する
- 赤のメッシュは後進可到達領域
- あるオートパイロットの状態が後進可到達領域に達した時にオートパイロットが動作し軌跡を変える
- 状態が高次元な場合に計算量が増大するという問題に対して様々なアプローチが提案されている
- 車両の導線に制約 (道路の上のみを動くなど)を入れる -> 車両の制御においては実用的だが航空ロボットにおいては非現実的
- システムの時間発展を線形近似 -> 近似精度が問題
- 微分方程式の単調増加性など数学的性質を利用
- 高次元の微分方程式を複数のグループに分け, グループごとに微分方程式を解く
- その他のアプローチとしてオフラインでの計算を利用するアプローチ, 機械学習モデルを使うアプローチがある
- オフラインでの計算を利用するアプローチとして事前にワーストケースの誤差 (Tracking error bound)を計算しておく手法がある
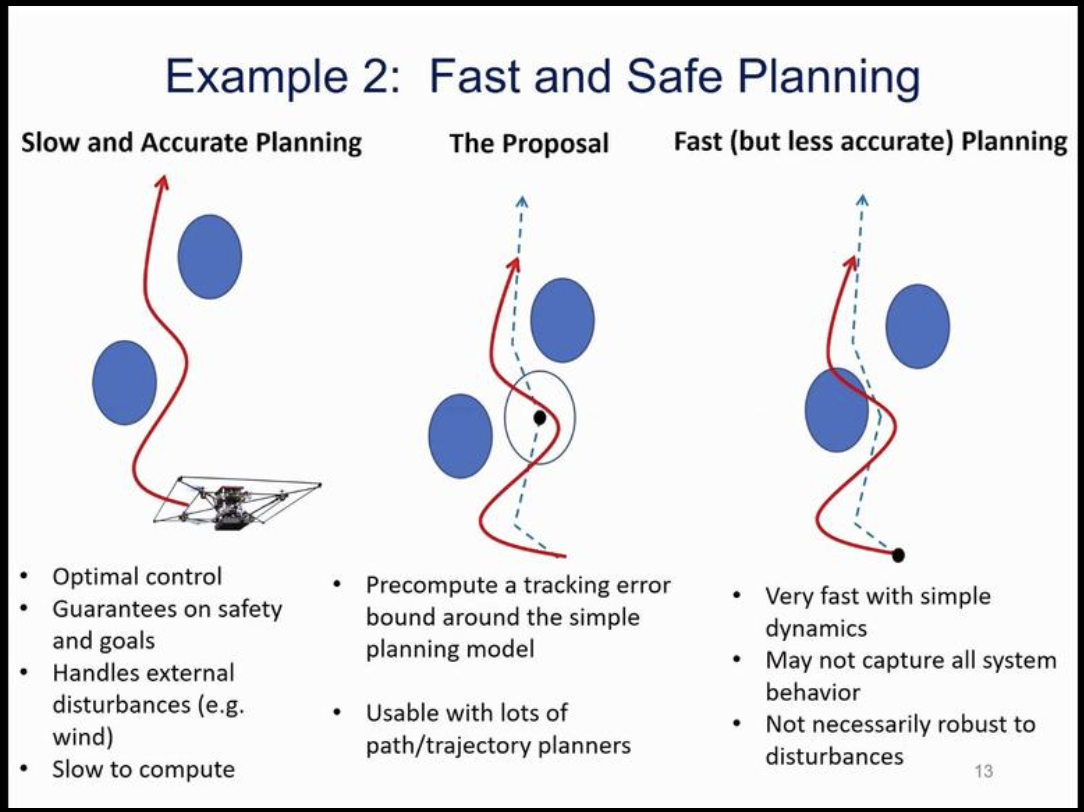
- Tomlin氏のチームでは歩行者との衝突回避というタスクにおいてTracking error boundと歩行予測モデルを利用する手法を提案 参考
- 歩行中の人がいる場所でクアッドロータを飛ばすケースを考える
- 衝突を避けるため, 歩行者が次の数ステップでどの場所に移動するか予測する
- 予測の誤差を考慮するため歩行予測に確率分布を仮定したボルツマンモデルを使う
- 人が歩く方向 \(u-H\)を \(P(u_H \vert x; \theta, \beta) = e^{\beta Q(x, u_H; \theta)}\)でモデル化
- \(\theta\)は歩行目標 (人の動きから推定)
- 歩行中の学生が2人いる状況で2台のクワッドローターを飛ばす実験を行った
- クワッドローターは2人の学生の動きをボルツマンマシンで予測し衝突を回避するための軌跡をうまく選ぶことができていた
- パラメータ \(\beta\)は各々の学生の動きに合わせてオンラインで更新
- ハミルトン-ヤコビ-アイザック方程式の解 \(J(x,t)\)をニューラルネットで近似する手法 DeepReach (ICRA 2021)を提案
- ランダムサンプルした入力に対しニューラルネットの出力を計算し, その出力が方程式を満たす様にニューラルネットのパラメータを学習
- 微分の情報を利用するため SIREN (活性化関数としてsin関数を用いたニューラルネット)を使用
- 3台の飛行機の3次元空間における衝突回避, 5台の車の2次元空間における衝突回避において既存の近似手法よりも正確な解が得られることを示した
Keynote: Automated Mechanism Design for Strategic Classification
by Vincent Conitzer (Duke University)
- ローン貸与, 採用, 収監期間の決定など様々な意思決定が人工知能によって行われるようになっている
- 人工知能によるアルゴリズムは情報の出し方を変えることで攻略できる
- 履歴書から特定の項目を削る, 経歴を詐称する, 文章の書き方を変えるなど
- すなわち「嘘をつく」インセンティブがある(見破られる場合もある)
- 人工知能アルゴリズムはそもそもバイアスがかかっているが, 攻略可能であることでさらなる不平等が生じる
- 攻略しやすい環境にいるエージェントとそれ以外のエージェントの差
- 例えばAI研究者が多い国や裕福な家の子供は有利になる
- メカニズムデザイン (制度設計理論)はミクロ経済学の一分野
- ゴールは利己的なエージェント (人)が集団の利益を最大化するような意思決定をするためのルールを決めること
- メカニズムデザイン=逆ゲーム理論 (Inversed game theory)と考えることもできる
- ゲーム理論ではルールが与えられた上で結果を分析するが, メカニズムデザインでは望ましい結果を得ることができるようなルールを設計する
- アルゴリズム設計者は公平性, 効率性が担保できるよう上手くアルゴリズムを設計する必要がある
- 例: 嘘をつくインセンティブが発生しないアルゴリズム
- この分野は近年ノーベル経済の受賞も続いており, 注目度も上がっている
- 2012年 マッチングメカニズムの理論とその実践に関する業績 (ロイド・シャプレイとアルビン・ロス)
- 2020年 オークションのメカニズムデザインの研究と実用化への貢献 (ポール・ミルグロム, ロバート・ウィルソン)
- これらの理論はエージェントが制限なく嘘をつけるケースにおいて考案されたもの
- Conitzer氏はつける嘘にある程度制限があるケースに焦点を当て研究を行なっている
- 例えばローンの借入においてエージェント (借入申請者)は自分の財務状況について虚偽の申請ができる
- 例: 友人からお金を借りて銀行口座の残高を一時的に多く見せる
- しかし多額の借金を抱え仕事を持たない人が, 安定したキャリアを持つ裕福な人の真似をすることは一般的に難しい (友人から借りれる額も限られる)
- すべてのエージェントが虚偽申請によって他のタイプ (負債額によるカテゴリ)になりすますことはできない
- 例: 2000ドルの負債がある人は友人から1000ドル借りて負債を1000ドルに見せかけることができる. しかし0ドルに見せかけることはできない
- つまり各タイプは虚偽申請ができる限られたタイプを持っている
- Conitzerらは2015年の研究でこのような場合においては問題がさらに難しくなる (顕示原理が成立しなくなる)ことを示した
- さらに, そのような場合にもTransitivityが保証される場合においては顕示原理が成り立つことを証明
- 2021年の研究では, いくつかのケースにおいてメカニズムデザインの問題が最小カット問題に帰着することを示した
- 例) ローンの借入 (借入申請者は全員ローンを借りたい)
- 提案アルゴリズムではまず虚偽申請の可否に基づいて重みつき有向グラフを構築する
- ノード=タイプ, ノードの値=そのタイプを受け入れた場合にどの程度利益を生むか
- 虚偽申請が可能なパスを重さ \(\infty\)のエッジでつなぐ
- グラフにSourceノードとTargetノードを追加しSourceノードにネガティブなノード, Targetノードにポジティブなノードを結合
- ノードの値の絶対値を追加したエッジの重みとする
- 構築したグラフに対してs-t最小カットを見つけ, 見つけた最小カットに基づいてメカニズムを構築する
- ローン借入の例なら, カットの片側のエージェントについてはローン申請を受け入れ, もう片側については拒否する
- この結果はすべてのタイプが結果に対して同じ嗜好を持っている場合に多クラス (出力がローンの借入可否などの2クラスではなく3クラス以上)にも拡張できる
- \(\infty\)の容量を持つエッジを使ったのは, あるタイプ (タイプ1)のエージェントが結果を得た場合, タイプ1と虚偽申請できる別のタイプ (タイプ2)のエージェントが少なくとも同等の結果を得ることを保証するため