Physics-informed neural networks with hard constraints for inverse design
タスク
- メタマテリアルの形状を特定の機能に合わせて設計したい
- メタマテリアルは音響, 力学, 熱・電子輸送, 電磁気・光学など, 工学のさまざまな分野で利用されている
- 設計空間が非常に高次元 (数百万から数十億のパラメータ)なのが困難な点
既存手法
- 対象の機能を目的関数として設定し, 偏微分方程式 (PDE)の制約下で最適化を行うアプローチがある
- PDE制約付き逆設計問題を解くために様々な数値計算手法が開発されてきた
- この論文において, 順問題=偏微分方程式求解, 逆問題=偏微分方程式のパラメータ推定, 逆設計=観測されない物理量の推定 と思われる
- 伝統的な手法は数値PDEソルバー (近似またはブルートフォース)に基づくもの
- 大規模最適化を行う場合は勾配を用いた最適化アルゴリズムが用いられる (アドジョイント法)
- 最近はPDEソルバの代わりにニューラルネットを用いる手法が提案されている
- ただしニューラルネットを用いた手法は膨大な量のデータが必要
- ニューラルネットを用いて設計候補を生成し, これを数値ソルバーで評価する手法 (教師なし学習や強化学習)も提案されている
- しかし, これらのアプローチはすべて従来の数値PDEソルバに依存している
提案手法
- 伝統的なPDEソルバに代わる手法として Physics-informed neural networks (PINNs)を提案
- 従来の数値計算法では逆問題と逆設計は似たような方法で解けるが, 提案手法 PINNにおいては逆設計 (観測されない物理量の推定)が問題になる
- これを解決するため, PDE制約付き逆設計を解くためのハード制約付きPINN法 (hPINN)を構築
- hPINNでは不等式制約も考慮
- 等式制約と不等式制約をハード制約として課すアプローチとして, ペナルティ法と拡張ラグランジュ法の2つを考える
- 以下のPDEに従う物理系を考える
\(\mathcal{F}[{\bf u}({\bf x}),\gamma({\bf x})]={\bf 0}\), \(\mathcal{B}[{\bf u}({\bf x})]\)- ここで \({\bf x}\)は任意の座標点, \(\mathcal{F}\)は任意のPDE演算子, \(\mathcal{B}\)は任意の境界条件
- \({\bf u}({\bf x})\)はPDEの解であり, パラメータ \(\gamma({\bf x})\)で決まる
- 既存手法では数値積分を用いてPDEを解くことでパラメータ \(\gamma\)についての解 \({\bf u}({\bf x})\)を得る
- 提案手法 PINNではPDEの解 \({\bf u}({\bf x})\)をニューラルネット \(\hat{\bf u}({\bf x})\)で近似
- さらにパラメータ \(\gamma\)を座標点 \({\bf x}\)を入力とするニューラルネット \(\hat{\gamma}({\bf x})\)でモデル化
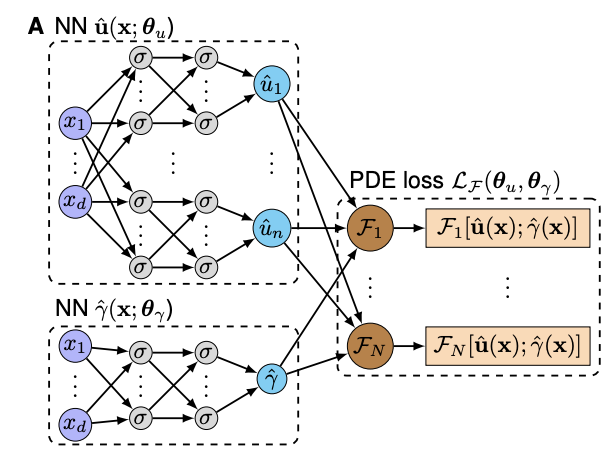
- \({\bf u}\)の観測値と推定値の誤差 \(\mathcal{J}({\bf u}; \gamma)\)を最小化するようなニューラルネット関数 \(\hat{\bf u}\), \(\hat{\gamma}\)のパラメータを学習
- さらにニューラルネット \(\hat{\bf u}\)と \(\hat{\gamma}\)がPDEの制約を満たすよう, 目的関数に以下のペナルティ項を加える
\(\mathcal{L}_F = \sum_{j=1}^M\mathcal{F}[\hat{\bf u}({\bf x}_j),\hat{\gamma}({\bf x}_j)]\)- \({\bf x}_j\)は入力座標空間における任意の点
- グリッドでもよいし一様分布からランダムにサンプルしてもよい
- 今回はサンプル \({\bf x}_j\)を生成するためSobol sequenceを使用
- この項は「等式制約がどれだけ満たされていないか」を表す
- PDE \(\mathcal{F}\)にはニューラルネット \(\hat{\bf u}({\bf x})\)の入力 \({\bf x}\)についての微分 \(\Delta\hat{\bf u}\)が含まれるが, これは自動微分を用いて計算できる
- \({\bf x}_j\)は入力座標空間における任意の点
- 境界条件 \(\mathcal{B}\)については, \(\hat{\bf u}\)をニューラルネットの出力 \(\mathcal{N}({\bf x})\)と条件式 \(l({\bf x})\)の複合関数で置き換えることで自然に考慮することができる
- 論文中では不等式制約 \(h({\bf u},\gamma)\leq 0\)がある場合も想定し, \(\mathcal{L}_F\)と同様の方法で \(\mathcal{L}_h\)を定義
- PINNの目的関数は \(\mathcal{L}=\mathcal{J}+\mu_F\mathcal{L}_F+\mu_h\mathcal{L}_h\)で定義される
- \(\mu_F\), \(\mu_h\)はペナルティ項の重要度を表す係数
- ソフトな制約を考える場合は \(\mathcal{L}\)をそのまま目的関数として使えばよい
- よりハードな制約を課したい場合, ペナルティ法もしくは拡張ラグランジュ乗数法を適用する
- ペナルティ法を用いる場合, ペナルティ項の係数 \(\mu\)の値を徐々に大きくしていきながら最適化を繰り返す
- 拡張ラグランジュ乗数法を用いる場合, 上述のペナルティ項付き損失関数にラグランジュ乗数項を足したもの (=拡張ラグランジュ関数)を目的関数として用いる
- ペナルティ法と同様 \(\mu\)の値を徐々に大きくしていくが, \(\lambda\)の更新が加わっている分制約が満たされた状態に近づく
実験
- 光学分野, 流体分野の2つの逆設計問題において提案手法 PINNの評価を行う
- まず, 深さ方向の画像に対するホログラフィ (光の回折と干渉を利用した立体画像の記録再生)という難しい問題を考える
- ホログラフィでは, コヒーレントな光 (レーザー)を物体に当て, その散乱光 (物体光)とレーザー光 (参照光)を同時に写真乾板に入射し, その干渉縞を記録する
- 散乱面に平行な像のホログラムはフーリエ光学に基づいてアルゴリズムを設計できるが, 深さ方向のホログラムではマクスウェル方程式に基づいて逆設計を行う必要がある
- 実験では, 電磁波 \(E\)の実数部分 \(\mathfrak{R}[E]\)と虚数部分 \(\mathfrak{I}[E]\), 波長を表すパラメータ \(\epsilon\)を良く近似するニューラルネット関数を導入し, マクスウェル方程式の制約下でそれらのニューラルネットのパラメータの最適化を行う
- 図3を見ると, 提案手法 hPINNの解 (図3A, 3B)が有限差分周波数領域 (FDFD)法で得られた参照解と一致していることがわかる
- 次に, 提案したhPINNを用いて, ストークス流における流体のトポロジー最適化の問題を解く
- 図7では提案手法 PINNと2つの数値PDEソルバ (FDFD, FEM)を比較
- hPINNによる設計 (図7C)はFDFD (図7D)やFEM (図7E)の結果よりも滑らかで簡素
- 勾配降下法を用いたニューラルネットワークには暗黙的に正則化が入っており, 滑らかな解に収束する傾向があるためと考察できる
- 図7では提案手法 PINNと2つの数値PDEソルバ (FDFD, FEM)を比較